Publications

Introduction

This paper describes a mathematically rigorous approach for defining market and credit stresses given a set of economic stresses. This approach is directly applicable to regulatory stress-test reporting.

Recent regulations such as CCAR and Basel III have adapted the long-standing risk measurement approach of stress-testing and made it applicable to new regulatory purposes. The current regulations require institutions to estimate losses in a base-case and in a stressed condition in which the condition is defined by stresses on a selection of macro-economic variables such as GDP and interest rates. A very direct estimate of the risk can then be obtained by using risk models that include economic and market conditions, for example regressions on historical default data where market conditions are included in the regressors¹, or cashflow simulation where the cashflows are conditional on factors such as vacancy and rental rates. However, these direct approaches require the estimation of the remaining market conditions or credit factors that are not already specified in the regulatory stress.

Approach

As an example, consider the task of assessing the increased risk of loans to commercial offices in Pittsburgh, conditional on a set of regulatory stresses. Intuitively we know that if macro factors such as GDP are depressed, then market factors such as rents and vacancy rates will also tend to be worse. However, for any given level of GDP, the exact change in the market factors will be uncertain, e.g., if GDP was down 4%, rents might fall 10% on some occasions or 25% on others. More formally, defining the overall economic conditions removes much of the systemic risk, but leaves idiosyncratic risk². The task then is to define the probability distribution of the market factors conditional on the fixed stressed levels defined for the economic factors.

The solution to this can be obtained by describing the interaction of the economic and macro factors using vector auto regression (VAR). The core VAR equation is as follows³:

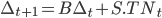
Where:

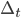• is the level of the economic and market factors relative to the forecast at time
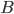• is the matrix of regressions showing how factors at one time step affect levels at the following time step
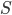• is the standard deviation of the exogenous shocks
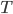• is the transformation matrix describing how individual shocks commonly affect multiple economic and market factors
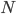• is a vector of Normally distributed exogenous shocks

This equation can then be broken down and rearranged to separate the factors that are de-fined as being stressed from the factors that are still to be determined. In the arrangement below, E represents the set of stresses to the economic factors given by the regulators and M represents the change in the remaining market factors that are still to be determined.

This can be rearranged to give:

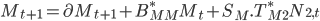
where

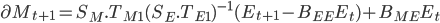
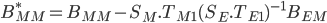
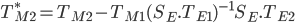
Here

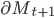• is an offset and along with 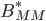defines the new depressed central forecast for the market factors
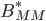• defines the relationship between the market factors at one time step given the market factors at the previous time step and given that there are no remaining uncertainties from the economic factors
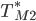• defines the correlation of the remaining shocks on the market factors

Results

The result of using this approach is that there are new depressed forecasts for the market factors and new probability distribution for the residual idiosyncratic shocks. Importantly, these residual shocks are correlated and the standard deviation of the shocks in the conditional case is less than in the unconditional base case. This means there is not double counting of depressed market forecasts plus full uncertainty on the market factors.

Graphically the effect is illustrated below. The first set of graphs shows the probability distribution of market factors in the stressed (conditional) case, compared with the distribution in the unstressed (unconditional) case⁴.

The graph below shows how the stressed scenarios are translated by the risk models into increased estimates of loss.

Given the limitations of historical data sets, there are some practical issues involved in the data analysis, but this approach has been used successfully in defining stresses to be used for regulatory reporting.

Conclusion

This framework gives a rigorous mathematical definition of how to define stressed credit and market scenarios conditional upon known stresses for economic factors. Although the equations are arithmetically complex, they are relatively easy to implement and point the way to correctly defining what is meant by a stress-test.