Introduction
Exercises such as CCAR are asking for loss forecasts to be allocated to individual quarters. If the requirement is to fully characterize the quarterly risk for individual loans, it is necessary to use risk models that are built using quarterly time steps. However, by their nature, CRE loan losses respond more slowly to economic conditions than other types of loans and therefore at the aggregate portfolio-level the difference between quarterly and annual pictures is less marked than for other assets. This means that at the portfolio level, there are several effective approaches for allocating annual estimates of risk to individual quarters. This paper illustrates three example approaches.
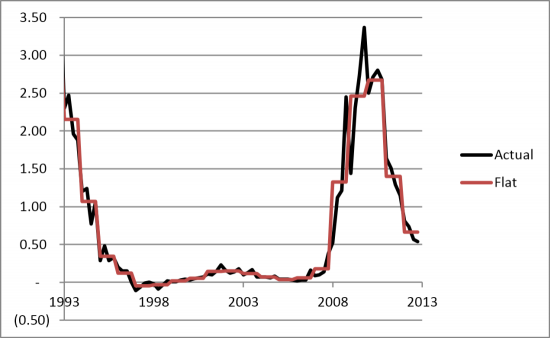
As a base-line, consider the simple algorithm of dividing the annual loss by four and making the 'flat' assumption that all the quarters within the year have the same loss. Figure 1 illustrates this for US Charge-offs from 1993 to 2013 and compares the actual quarterly data with the annual flat averages. By definition the annual averages track the overall trend, but there are some quarters where the loss spikes significantly away from the annual average. This difference is a combination of actual response to quarterly economic conditions, plus some idiosyncratic randomness (e.g., weather, a particular government statement, or the idiosyncratic risk of the individual loans).
Figure 1. US Quarterly CRE Charge-off rates compared with the Flat Annual Average1
As alternatives to this flat allocation, three methods are illustrated in this paper:
- Smoothed Allocation
- Difference of Models
- Model of Differences
Smoothed Allocation
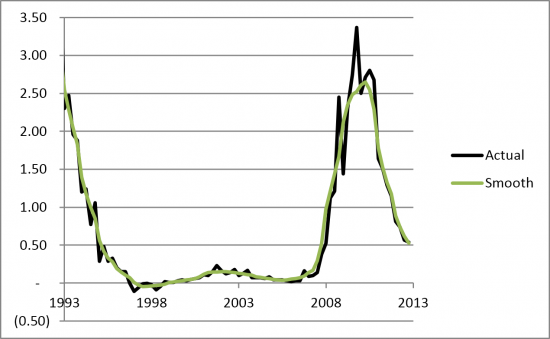
Smoothed allocation takes the flat allocation for each quarter and then calculates the exponentially weighted running average to define a new quarterly loss. This has the effect of taking the 'edges' off the flat average and, given the strong auto correlation in losses, it feeds information across the annual time steps to better match the underlying trends. This is illustrated in Figure 2 below where the smoothed average stays close to the actual data for most quarters.
Figure 2. US Quarterly CRE Charge-off rates compared with the Smoothed Allocation
Difference of Models
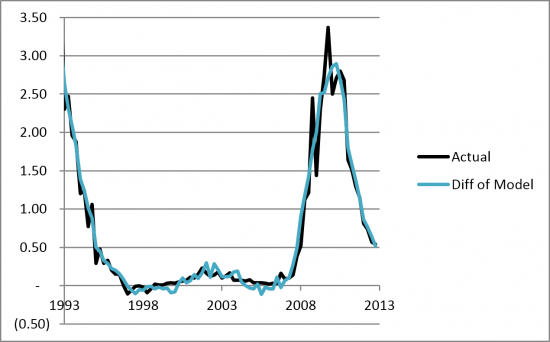
For the Difference of Models, the approach is to build a model estimating smoothed losses based on quarterly economic data and then build a second model estimating quarterly losses based on quarterly economic data. We then take the difference between the two and add that to the smoothed annual model.
The result is very similar to the Model of Differences although the Difference of Models has less 'chatter' in the times of low defaults as illustrated in Figure 3.
Figure 3. US Quarterly CRE Charge-off rates compared with the Difference of Models
Model of Differences
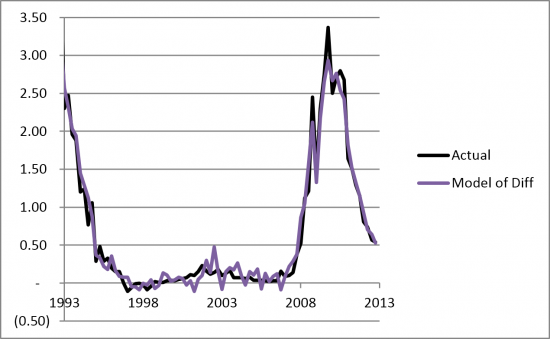
The Model of Differences looks at the historical difference between the quarterly loss and the smoothed average and regresses this difference against the historical difference between quarterly economic data and the smoothed average of the economic data. This provides a model for how a quarter's loss will vary from the smoothed loss based on how quarterly economic conditions vary from their smoothed average. Note that this can also include lagged economic conditions, e.g., if an unusual drop in GDP one quarter causes an unusual spike in losses three quarters later. Figure 4 below illustrates the improvement in the fit, especially in the crisis period from 2008.
Figure 4. US Quarterly CRE Charge-off rates compared with the Model of Differences
Comparison of Approaches
Table 1 below compares the approaches based on the standard deviation of the residual between the models' estimate and the actual loss at each quarterly time step.
Table 1. Standard deviation of difference between model and quarterly loss (bps)
| '' | Flat Allocation | Smoothed Allocation | Difference of Models | Model of Differences |
|---|---|---|---|---|
| 1993 - 2013 | 0.25 | 0.21 | 0.19 | 0.17 |
| 2008 - 2013 | 0.47 | 0.35 | 0.30 | 0.20 |
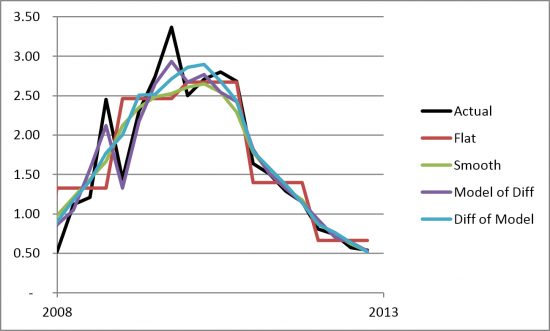
The Model of Differences minimizes the standard deviation across the cycle as a whole, and especially during the crisis period as illustrated in Figure 5.
Figure 5. US Quarterly CRE Charge-off rates compared with Models 2008-2013
Summary and Conclusions
This paper shows that there are reasonable approaches for taking annual loss estimates and allocating them out to quarters if needed. These models are illustrative, and more extensive work could easily improve upon them. However, before launching into a mission to build the perfect quarterly model, consider Figure 6. Figure 6 shows the cumulative loss estimates starting in Q1 2008.
Figure 6. Comparison of Approaches in Estimating Cumulative Losses
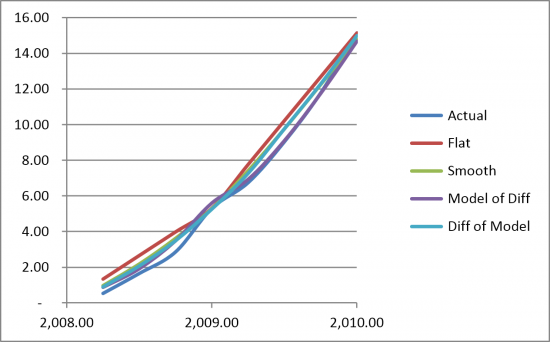
The first point to be made is that at the annual vertices, all the models give the same result for the cumulative loss. The second point is that the simple flat approach is the most conservative in a time of increasing losses because it anticipates losses from later in the year.
The approaches in this paper are reasonable ways to allocate risk to individual quarters, but we should not lose sight of the fact that for commercial real estate assets, it is the cumulative loss over two or more years that destroys banks so it is most important that risk models should give good estimates of the medium to long term risks.
Dr. Chris Marrison
CEO, Risk Integrated
Contact Risk Integrated today
Want to learn more about this article? Speak to our experts today.
Contact Us